Single unit templates
Many of these are taken from our papers, including their Supplementary Materials. Remember that these are just the basic building units, and not necessarily an end in themselves.
A 2-4 kirigami cut joining a ~5~7 cut via pure climb, with both the triangular lattice and hexagonal lattice shown. The presence of Greek letters indicates that you're doing something highly technical.
Another 2-4 and ~5~7 kirigami climb, this time without the distractions.
A climb pair of two ~5~7 kirigami cuts.

Two ~5~7 cuts connected by glide, with a handy picture of the final product.
The same but without the distractions.
The path that joins the two excised wedges doesn't need to be straight. Here there's a ratchet effect.
Part glide, part climb linking two ~5~7's.
Mixed climb and glide between ~5~7 pairs. Cut the wedges then according to just one colour of either burgundy, grey or blue. In each case the final structure will be the same, only differing in the scar along the rejoined cuts. Note that at all places along the lines, the lines between top corners is exactly one unit higher than the line between bottom corners.
Who says that only two dislocations can cancel simultaneously? Note that the Burgers vectors sum to zero (form a triangle).
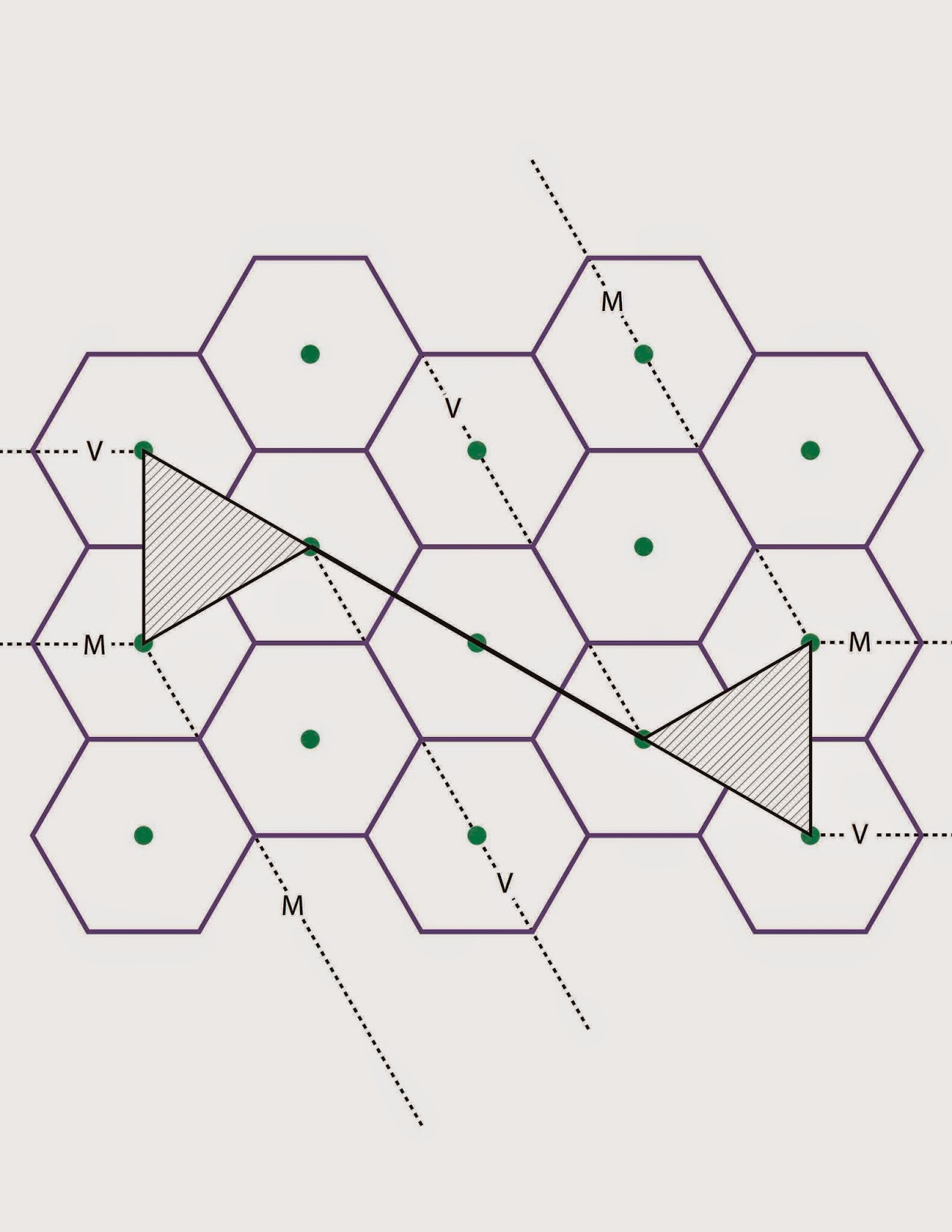
Ready to design your own? Here's a hexagonal grid with centres marked. Get some in custom sizes from http://incompetech.com/graphpaper/hexagonal/.
Multiple unit templates
Here's a part of a sixon array. Cut out the hexagons this time, and fold across the red lines.

A larger area of a similar glide design.
The same design, without the underlying lattice. A vector version of this is what you feed to a laser cutter.
Flat-topped mushroom field. Cut out the reddish areas and deduce the fold lines for yourself.
Hint: there are 12 per hexagon.